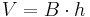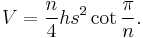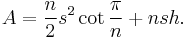Prism (geometry)

Set of uniform prisms

(A hexagonal prism is shown)
Type uniform polyhedron
Faces 2+n total:
2 {n}
n {4}
Edges 3n
Vertices 2n
Schläfli symbol {p}x{} or t{2, n}
Coxeter-Dynkin diagram
Vertex configuration 4.4.n
Symmetry group Dnh, [n,2], (*22n), order 2n
Dual polyhedron bipyramids
Properties convex, semi-regular vertex-transitive

n-gonal prism net (n = 9 here)

In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy (not in the same plane as the first), and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a pentagonal prism. The prisms are a subclass of the prismatoids.

Contents

General, right and uniform prisms

A right prism is a prism in which the joining edges and faces are perpendicular to the base faces. This applies if the joining faces are rectangular. If the joining edges and faces are not perpendicular to the base faces, it is called an oblique prism.

Some texts may apply the term rectangular prism or square prism to both a right rectangular-sided prism and a right square-sided prism. The term uniform prism can be used for a right prism with square sides, since such prisms are in the set of uniform polyhedra.

An n-prism, having regular polygon ends and rectangular sides, approaches a cylindrical solid as n approaches infinity.

Right prisms with regular bases and equal edge lengths form one of the two infinite series of semiregular polyhedra, the other series being the antiprisms.

The dual of a right prism is a bipyramid.

A parallelepiped is a prism of which the base is a parallelogram, or equivalently a polyhedron with 6 faces which are all parallelograms.

A right rectangular prism is also called a cuboid, or informally a rectangular box. A right square prism is simply a square box, and may also be called a square cuboid.

An equilateral square prism is simply a cube.

Volume

The volume of a prism is the product of the area of the base and the distance between the two base faces, or the height (in the case of a non-right prism, note that this means the perpendicular distance).

The volume is therefore:

V = B \cdot h

where B is the base area and h is the height. The volume of a prism whose base is a regular n-sided polygon with side length s is therefore:

V = \frac{n}{4}hs^2 \cot\frac{\pi}{n}.

Surface area

The surface area of a right prism is 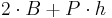2\cdot B %2B P\cdot h, where B is the area of the base, h the height, and P the base perimeter.

The surface area of a right prism whose base is a regular n-sided polygon with side length s and height h is therefore:

A = \frac{n}{2} s^2 \cot{\frac{\pi}{n}} %2B n s h.

Symmetry

The symmetry group of a right n-sided prism with regular base is Dnh of order 4n, except in the case of a cube, which has the larger symmetry group Oh of order 47, which has three versions of D4h as subgroups. The rotation group is Dn of order 2n, except in the case of a cube, which has the larger symmetry group O of order 24, which has three versions of D4 as subgroups.

The symmetry group Dnh contains inversion iff n is even.

Prismatic polytope

A prismatic polytope is a dimensional generalization of a prism. An n-dimensional prismatic polytope is constructed from two (n − 1)-dimensional polytopes, translated into the next dimension.

The prismatic n-polytope elements are doubled from the (n − 1)-polytope elements and then creating new elements from the next lower element.

Take an n-polytope with fi i-face elements (i = 0, ,..., n). Its (n + 1)-polytope prism will have 2fi + fi−1 i-face elements. (With f−1 = 0, fn = 1.)

By dimension:

Uniform prismatic polytope

A regular n-polytope represented by Schläfli symbol {p, q, ..., t} can form a uniform prismatic (n + 1)-polytope represented by a Cartesian product of two Schläfli symbols: {p, q, ..., t}x{}.

By dimension:

Higher order prismatic polytopes also exist as Cartesian products of any two polytopes. The dimension of a polytope is the product of the dimensions of the elements. The first example of these exist in 4-dimensional space are called duoprisms as the product of two polygons. Regular duoprisms are represented as {p}×{q}.

See also

External links

Platonic solids (regular)
Archimedean solids
(Semiregular/Uniform)
Catalan solids
(Dual semiregular)
Dihedral regular
Dihedral uniform
prisms · antiprisms
Duals of dihedral uniform
Dihedral others
Degenerate polyhedra are in italics.